Tree:
Main concept for the tree.
-Data.
-Pointer to left child.
-Pointer to right child.
Common Terminology
-Node - A Tree node is a component which may contain it’s own values, and references to other nodes
-Root - The root is the node at the beginning of the tree
-K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2.
-Left - A reference to one child node, in a binary tree
-Right - A reference to the other child node, in a binary tree
-Edge - The edge in a tree is the link between a parent and child node
-Leaf - A leaf is a node that does not have any children
-Height - The height of a tree is the number of edges from the root to the furthest leaf
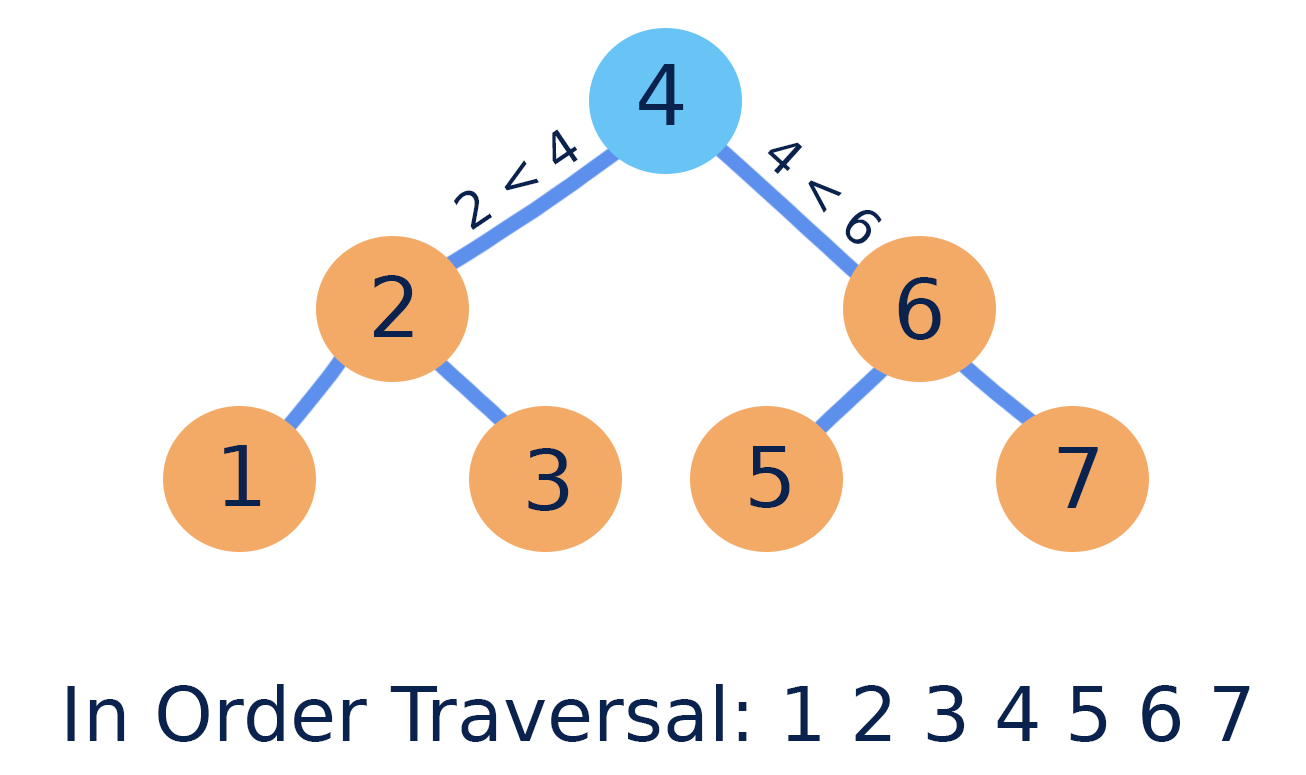
Traversals:
An important aspect of trees is how to traverse them. Traversing a tree allows us to search for a node, print out the contents of a tree, and much more! There are two categories of traversals when it comes to trees:
Depth first:
traversal is where we prioritize going through the depth (height) of the tree first.
Breadth Firs:
Breadth first traversal iterates through the tree by going through each level of the tree node-by-node.
K-ary Trees:
If Nodes are able have more than 2 child nodes, we call the tree that contains them a K-ary Tree. In this type of tree we use K to refer to the maximum number of children that each Node is able to have.
Binary Search Trees:
A Binary Search Tree (BST) is a type of tree that does have some structure attached to it. In a BST, nodes are organized in a manner where all values that are smaller than the root are placed to the left, and all values that are larger than the root are placed to the right.
Adding a node:
Because there are no structural rules for where nodes are “supposed to go” in a binary tree, it really doesn’t matter where a new node gets placed.
One strategy for adding a new node to a binary tree is to fill all “child” spots from the top down. To do so, we would leverage the use of breadth-first traversal. During the traversal, we find the first node that does not have 2 child nodes, and insert the new node as a child. We fill the child slots from left to right.
In the event you would like to have a node placed in a specific location, you need to reference both the new node to create, and the parent node upon which the child is attached to.
Big O:
The Big O time complexity of a Binary Search Tree’s insertion and search operations is O(h), or O(height). In the worst case, we will have to search all the way down to a leaf, which will require searching through as many nodes as the tree is tall. In a balanced (or “perfect”) tree, the height of the tree is log(n). In an unbalanced tree, the worst case height of the tree is n.
Resources:
Done by Omar-zoubi